BLÅVALSTÄNK
Den väger 2,7 ton. Tungan alltså.
Min lilla fyra och jag tänkte att varje elev vägde 50 kilo. Vi tror nu att vi behöver två stora elevklasser för att viktåskådliggöra valens tunga...
Anne-Marie
som väger en aning mer men vi avrundar gladeligen både uppåt och nedåt då vi har praktisk matematik.
HUR VÄGER MAN EN BLÅVAL?
Det är dagens fråga i min lilla fyra.
Anne-Marie
MATEMATIK SOM POESI...
Jag har gjort matematikpoesi. Så nu ska jag leta reda på något exempel som åskådliggör det.
Men vad sägs om inledningen till en roman jag läste i utlandet
Blue nines and red fours...
Det får mig att gå igång ... fantasin får näring...
Blåa nior på march i uniform,
röda fyror som stolar vid uteserveringens solbelysta bord...
Anne-Marie
GENRER är en ORDNING

Att förstå en genre är att skapa en slags ordning.
Vad är det jag kan förvänta mig?
En slags rubrik på ett innehåll.
Medvetenhet om genrer bidrar också till kritiskt tänkande.
Genren kan ses som en kategorisering av budskapen...
Jag läser just nu boken TIDSKRIFTSDESIGN av Eva Jais-Nielsen. Det är en ... ja... en faktabok, tänker jag. En bok om hur att förstå en hel tidnings uppbyggnad, form och hur allt syftar till att kommunicera med läsaren. Först gäller det ju att locka läsaren till sig - med omslag, puffar och välkänd logga.
Men jag läser om bilder, fotografier och illustrationer.
Ett fotografi i en tidning kan delas in i fler genrer:
Faktabilder
Faktadokumentära bilder
Dokumentära bilder (reportagebilder)
Prosadokumentära bilder
Prosabilder
Poesibilder
Prosapoetiska bilder
Naturbilder
Det som är viktigt att känna till är att genrer har en tendens att försvinna in i en annan genrer och att genrer blandas samman och skapar en ny genre. Här talar vi fotografi och genrer - ämnet är alltså gigantiskt stort.
Vad är en matematikbok? Hur definierar vi den? Vilken genre? Varför det?
Anne-Marie
PLÅSTRA OM MATEMATIKELEVEN
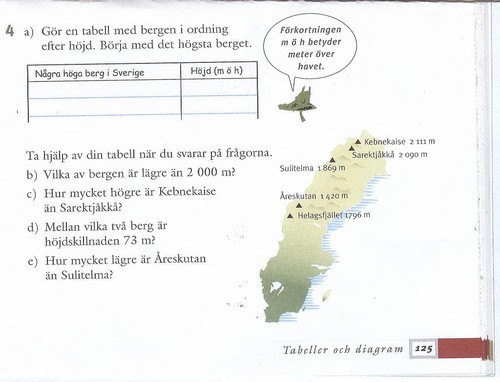
Men jag tittar på d-uppgiften.
Det är en bra uppgift. Jag tittar på språket. Jag vet att ordetn SKILLNAD - SKILLNADER - är begrepp som måste övas in länge, i alla sammanhang. Då man i andra sammanhang frågar - vad är skillnaden mellan päron och äpplen - så svarar eleverna ofta, alldeles för ofta, att äpplen är si eller så, och glömmer att jämföra med den andra och undersöka de olika egenskaperna och presentera - ja just det - skillnaderna. Det här tränar jag mina elever i jämt. Ordet SKILLNADER är svårbegripligt.
Så hur kan jag göra. Jo- jag kan modella att jag också får fundera ett tag innan jag kan lösa uppgiften. Det krävs lite tänk visar jag. En aning knep också, får jag visa. Jag undrar hur eleven tycker att jag ska gå tillväga. Hur tror du att jag kan lösa uppgiften? Därmed är ansvaret mitt. Inte elevens. Och eleven kommer att stötta mig, ge förslag och introducera någon möjlig väg att lösa det hela på. Och då ser jag hur jag ska lotsa eleven genom svårigheterna. För när vi samtalar så är vi nästan där - ja - att lösa fler problem än ett.
Anne-Marie,
som också tycker att strategin LÄS HÖGT FÖR DIG SJÄLV är en underskattad strategi. Och strategin GÅ OMKRING OCH TÄNK också är en underskattad strategi. Det är bara att tänka själv - det är svårt - hur gör jag? Jag talar högt för mig själv, börjar vandra omkring och göra annat, för att sedan plötsligt inse att jag är färdig med mitt tänk. Ibland tycker jag synd om elever.
TA DEL AV...
Anne-Marie
MATEMATIK UR BOKENS INNEHÅLLSREGISTER

Anne-Marie
som nu har skrivit 1/4378 inlägg.
LEKTIONSIDÉ MATEMATIK: fråga-svara

L E K T I O N S F Ö R S L A G
Lektionsförslag - En generell matematiklektionsidé som fungerar i alla årskurser
G E N O M F Ö R A N D E
1) Låt alla elever ta fram sina matematikböcker.
2) Sätt eleverna i en ring, de ska kunna se varandra.
3) Be eleverna slumpmässigt slå upp sina matematikböcker.
4) Modella (läraren visar genom att göra och delta i det som eleverna ska göra) genom att läsa en fråga ur matematikboken, vilken som helst.
5) Låt någon elev i gruppen svara (man ska inte lösa uppgiften men svara så att man får med enheter och ord från frågan)
6) Den som fått svara är nu den som ställer en fråga ur sin matematikbok, och så fortsätter vi hela ringen runt.
7) Läraren deltar naturligtvis, läraren får en fråga, modellar ett tänkt svar, och frågar i sin tur vidare.
S Y F T E T
Syftet med denna uppgift är att få eleverna att använda enheter och ord ur frågorna när de själva svarar i sina böcker, eller i framtida provuppgifter. Svaren ska var utförliga och många ord kan man låna direkt ut frågorna. Denna medvetenhet vill jag skapa hos mina elever.
S K A P A R F Ö R S T Å E L S E
Denna uppgift hjälper eleverna att lyssna till frågorna, muntligen uttrycka sig i enheter i utvecklad form, alltså inte m, utan meter, kilogram, decimeter, millimeter, inga förkortningar.
A V D R A M A T I S E R A R
Denna uppgift avdramatiserar också att man måste lösa talen eller uppgifterna. Det blir odramatiskt att skapa ett svar
när man får hitta på ett antal istället för att genast räkna ut det.
T E O R I
Jag är ju en god vän med gamle Lev Vygotskji och tar alla undervisande möjligheter att låta mina elever ta orden i sina munnar. De ska läsa uppgifter högt, fråga och diskutera för att senare kunna använda samma strategier i sitt självständiga tänk - och då får de gärna tala högt med sig själva (människan gör det då hon är i svårigheter eller har problem av något slag, är nära en lösning, då talar vi för oss själva - få se nu...om jag tar den där och sätter den här....). Det blir lättare att förstå om man får använda fler sinnen än bara synen. Talar man matematik så hör man också och därmed aktiverar man upp flera möjligheter att lära.
L Ä R A R E N K A N
Läraren kan höra hur eleverna förstår. Det blir mycket märkbart om en elev inte kan utläsa ex m.m utan famlar efter förståelse och begrepp. Detta ger läraren en indikation om att undersöka och stötta eleven i begrepp och förkortningar.
S T R Ä V A N S M Å L M E D A - M K O M M E N T A R E R
Muntlig matematik utvecklar och bidrar till att eleven når strävansmålen inom ämnet matematik. Jag har hämtat strävansmålen ur Skolverkets kursplaner:
Skolan skall i sin undervisning i matematik sträva efter att eleven
– utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och att använda matematik i olika situationer, (A-M tankar: Matematiken blir gemensam och väcker kollektiva funderingar vilket bidrar till ett ökat eller begynnande intresse för matematik då vi är muntliga).
– inser värdet av och använder matematikens uttrycksformer, (A-M tänker; Det är en absolut demokratisk rättighet att eleverna kan uttrycka sig såväl skriftligt som muntligt i matematiska termer och integrera detta i på ett naturligt sätt i ett aktivt språkbruk).
– utvecklar sin förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande, (A-M tänker: Denna enkla övning banar vägen för resonemang och diskussion och eleverna börjar tala och tänka matematik så det märks och hörs i klassrummet).
– utvecklar sin förmåga att formulera /.../ (A-M tänker; uppgifter som är muntliga tränar förmågan att formulera sig också skriftligt och utvecklar en matematisk säkerhet i muntligt tal).
– olika metoder, måttsystem och mätinstrument för att jämföra, uppskatta och bestämma storleken av viktiga storheter,(A-M tänker: Då vi talar matematik, eller gör som i denna enkla lektionsidé så använder vi ju inte förkortningarna utan lär oss att uttala dem i fullständig form och i det sammanhang de ska användas i).
– grundläggande geometriska begrepp, egenskaper, relationer och satser, (A-M tänker; Ja jag har nog sagt det redan, muntligheten hjälper, stäker och förstärker kunskaperna).
– grundläggande algebraiska begrepp, uttryck, formler, ekvationer och olikheter, (A-M tänker: Se tidigare).
– sannolikhetstänkande i konkreta slumpsituationer. (A-M tänker: Vi talar ofta sannolikhet och rimlighet i samband med att vi faktiskt också försöker oss på att gissa ut de rätta svaren utan att använda papper, räknare eller något annat hjälpmedel. Vi vågar gissa mer då vi gör den här fråga-svara matematiken. Då kommer man genast in på hur sannolikt svaret är).

Ja! Det var det! Då är det bara att sätta igång imorgon.
Anne-Marie
TVÅ STEG

Två steg över gränsen.
Fyra steg tillbaka in i värmen.
Åtta steg in i köket.
Fyra armrörelser för att sätta på kaffet.
Tolv steg till radion.
Fyra språng till sms:et i mobilen.
Två stapplande steg mot soffan.
Två greppande händer runt bokryggen.
En handsträckning mot kaffekoppen.
Söndagmorgon.
AnneMarie
KILO-GRAM
Idag talade eleverna spontant om vikter och använde begreppet kilogram för första gången.
Vägen till medvetenheten är banad.
Anne-Marie
HUR VÄGER MAN EN BLÅVAL?
H U R V Ä G E R M A N E N B L Å V A L ?
Hur gör man?
Hur kan man tänka?
Varför ska man väga en blåval?
Hur vet man att en blåval väger 180 ton?
Hur mycket är ungefär ett ton?
Anne-Marie
KILO är 1000

Ordet KILO betyder 1000!
Om ordet kilo betyder 1000 så är det ganska knepigt att säga
- Jag vill ha ett kilo ägg. Det blir väldigt många ägg.
- Jag ska köpa ett kilo äpplen. Det blir väldigt många äpplen. Ett tusental äpplen blir det.
- Jag vill ha ett kilogram äpplen. Det blir en aning mer lättburet. För ett kilogram äpplen är väl en aning färre än tusen äpplen. Man får väl en - sju-åtta äpplen på ett kilogram.
Så här talade vi idag. Muntlig matematik,
Vi ersatte alla 1000-ord med kilo.
- Jag har kilo förväntningar på den här dagen, sa jag som modellade det hela.
- Jag har kilo kronor sa en annan, och så fortsatte vi ringen runt.
Sen lade vi till gram. Vi talade vikter och kilogram.
- Jag väger 65 kilogram, sa jag sannenligt.
- Jag väger 165 kilogram, lekte en elev och så fortsatte det ringen runt.
Imorgon ska vi tala kilo-meter.
Då ska jag undersöka hur vi tänker kring kilo och meter.
Idag tror jag begreppet kilo fick en annan innebörd.
Jag har fler id´eer hur jag ska förankra detta viktiga vardagsbegrepp.
Anne-Marie
MATEMATIKBOKENS FAKTISKA INNEHÅLL

Jag funderar över matematikbokens innehåll.
Jag vet att eleverna INTE betraktar matematiktexter som sanna eller verkliga. Eleverna uppfattar inte texterna som konstruerade uppgifter som hör samman med geografi, samhällskunskap eller matematiknyttigheter i största allmänhet. Att de tänker så tror jag beror på att vi lärare inte gör matemtiktexterna levande och innehållsrika genom att modella undrande, modella högläsning, modella förundran, modella ifrågasättande, modella vår egen nyfikenhet på vad matematiktexter förmedlar.
Anne-Marie
MATEMATIK, MÖNSTER, SPRÅK

Anne-Marie
som dedicerar hela detta tänk och inlägg till en trogen matematikutvecklare som då och då läser min blogg.
MATEMATIK - PÅ MILLIMETERN MIG SJÄLV




Idag mäter vi oss. Ordentligt.
Hur långt är pekfingret, ett hårstrå, foten, stortån?
Hur långt är det mellan ankel och knä?
Hur långt är det mellan handled och armbåge?
Hur mycket mäter det runt ett pekfinger?
När vi mäter ... allt vi kan så kommer det frågor?
Vad är en ankel?
Vad börjar en hand?
Vad slutar nacken och var börjar ryggen?
Och upptäckterna låter först som Va? Hur kan det här stämma?
Va - tänk att mitt pekfinger mäter lika mycket som det mäter runt mitt pekfinger?
Foten mäter lika mycket som avståndet mellan armbågen och handen.
Det är språkligt, roligt, lärorikt, innehållrikt!
Det blir på elevernas vis som mätningarna äger rum.
Hur mäter man längden om man får välja själv?
Vilka redskap använder eleverna om de får välja fritt?
Vilka ord använder eleverna i sina samtal med varandra?
Det är bara att lärarlyssna!
Lektionen avslutades med en sammanslagning av samtliga mått. Då använde vi naturligtvis miniräknare och började förstå varför man skriver 32.5 cm ... och hur man skriver det i en miniräknare. Det är mycket kunskaper som behövs för att rätt använda ett hjälpmedel. För övrigt kommer vi nu långsamt arbeta oss in mot decimaltal.
Anne-Marie
som inte kunde ana att andra mäter samma sak fast med helt andra syften
http://www.dn.se/DNet/jsp/polopoly.jsp?a=873143
Matematik: ATT SVÄLJA SIN TUNGA


Anne-Marie
DEN BÄRANDE MATEMATIKTEXTEN


Anne-Marie,
FAKTA I MATEMATIKBOKEN

Det är nästan skrämmande att våra elever inte ser innehållet i Matematikboken som fakta, som innehållsbärande information. De räknar på och tänker inte på vad det är för information de räknar ut och vad detta kan innebära för kunskapshelheten. Det är information som vi räknar med.
I Matteborgen är det verkliga bergshöjder och riktiga havsdjup vi räknar med. Det är faktiskt information. Jag har utvecklat en idé hur att göra detta medvetet hos mina elever.
Genom att läraren är medveten om, gör undervisning kring, utvecklar interaktionen med matematikbokens text som eleverna kan få tillgång till HELA matteboken.
Det är genom att jag, läraren, fokuserar på innehållet, synliggör det bättre, funderar kring det mer aktivt. Jag har en plan...
Anne-Marie
VARFÖR INTE MINIRÄKNARE?


Anne-Marie
SPRÅKLIG MATEMATIK

Anne-Marie,
som citerar MATTEBORGEN 4 A, Bonnier Utbildning